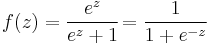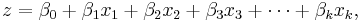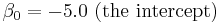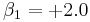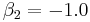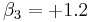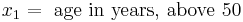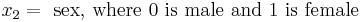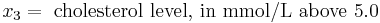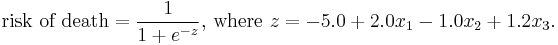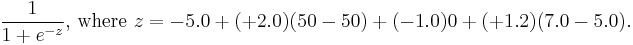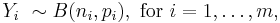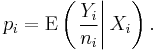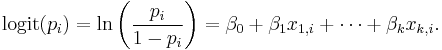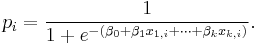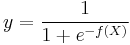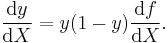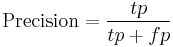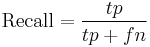Logistic regression

In statistics, logistic regression (sometimes called the logistic model or logit model) is used for prediction of the probability of occurrence of an event by fitting data to a logistic function. It is a generalized linear model used for binomial regression. Like many forms of regression analysis, it makes use of several predictor variables that may be either numerical or categorical. For example, the probability that a person has a heart attack within a specified time period might be predicted from knowledge of the person's age, sex and body mass index. Logistic regression is used extensively in the medical and social sciences fields, as well as marketing applications such as prediction of a customer's propensity to purchase a product or cease a subscription.

Contents

Definition

An explanation of logistic regression begins with an explanation of the logistic function, which, like probabilities, always takes on values between zero and one:

f(z) = \frac{e^{z}}{e^{z} %2B 1} \! = \frac{1}{1 %2B e^{-z}} \!

A graph of the function is shown in figure 1. The input is z and the output is ƒ(z). The logistic function is useful because it can take as an input any value from negative infinity to positive infinity, whereas the output is confined to values between 0 and 1. The variable z represents the exposure to some set of independent variables, while ƒ(z) represents the probability of a particular outcome, given that set of explanatory variables. The variable z is a measure of the total contribution of all the independent variables used in the model and is known as the logit.

The variable z is usually defined as

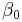z=\beta_0 %2B \beta_1x_1 %2B \beta_2x_2 %2B \beta_3x_3 %2B \cdots %2B \beta_kx_k,

where \beta_0 is called the "intercept" and 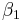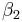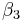\beta_1, \beta_2, \beta_3, and so on, are called the "regression coefficients" of 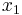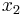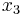x_1, x_2, x_3 respectively. The intercept is the value of z when the value of all independent variables are zero (e.g. the value of z in someone with no risk factors). Each of the regression coefficients describes the size of the contribution of that risk factor. A positive regression coefficient means that the explanatory variable increases the probability of the outcome, while a negative regression coefficient means that the variable decreases the probability of that outcome; a large regression coefficient means that the risk factor strongly influences the probability of that outcome, while a near-zero regression coefficient means that that risk factor has little influence on the probability of that outcome.

Logistic regression is a useful way of describing the relationship between one or more independent variables (e.g., age, sex, etc.) and a binary response variable, expressed as a probability, that has only two values, such as having cancer ("has cancer" or "doesn't have cancer") .

Sample size-dependent efficiency

Logistic regression tends to systematically overestimate odds ratios or beta coefficients when the sample size is less than about 500. With increasing sample size, the magnitude of overestimation diminishes and the estimated odds ratio asymptotically approaches the true population value. In a single study, overestimation due to small sample size might not have any relevance for the interpretation of the results, since it is much lower than the standard error of the estimate. However, if a number of small studies with systematically overestimated effects are pooled together without consideration of this effect, an effect may be perceived when in reality it does not exist.[1]

A minimum of 10 events per independent variable has been recommended.[2][3] For example, in a study where death is the outcome of interest, and 50 of 100 patients die, the maximum number of independent variables the model can support is 50/10 = 5.

Example

The application of a logistic regression may be illustrated using a fictitious example of death from heart disease. This simplified model uses only three risk factors (age, sex, and blood cholesterol level) to predict the 10-year risk of death from heart disease. These are the parameters that the data fit:

\beta_0=-5.0 \text{ (the intercept)}
\beta_1=%2B2.0
\beta_2=-1.0
\beta_3=%2B1.2
x_1=\text{ age in years, above 50}
x_2=\text{ sex, where 0 is male and 1 is female}
x_3=\text{ cholesterol level, in mmol/L above 5.0}

The model can hence be expressed as

\text{risk of death} = \frac{1}{1%2Be^{-z}} \text{, where } z=-5.0 %2B2.0x_1 -1.0x_2 %2B 1.2x_3.

In this model, increasing age is associated with an increasing risk of death from heart disease (z goes up by 2.0 for every year over the age of 50), female sex is associated with a decreased risk of death from heart disease (z goes down by 1.0 if the patient is female), and increasing cholesterol is associated with an increasing risk of death (z goes up by 1.2 for each 1 mmol/L increase in cholesterol above 5 mmol/L).

We wish to use this model to predict a particular subject's risk of death from heart disease: he is 50 years old and his cholesterol level is 7.0 mmol/L. The subject's risk of death is therefore

\frac{1}{1%2Be^{-z}} \text{, where } z=-5.0 %2B (%2B2.0)(50-50) %2B (-1.0)0 %2B (%2B1.2)(7.0-5.0).

This means that by this model, the subject's risk of dying from heart disease in the next 10 years is 0.07 (or 7%).

Formal mathematical specification

Logistic regression analyzes binomially distributed data of the form

Y_i \ \sim B(n_i,p_i),\text{ for }i = 1, \dots , m,

where the numbers of Bernoulli trials ni are known and the probabilities of success pi are unknown. An example of this distribution is the fraction of seeds (pi) that germinate after ni are planted.

The model proposes for each trial i there is a set of explanatory variables that might inform the final probability. These explanatory variables can be thought of as being in a k-dimensional vector Xi and the model then takes the form

p_i = \operatorname{E}\left(\left.\frac{Y_i}{n_{i}}\right|X_i \right). \,

The logits, natural logs of the odds, of the unknown binomial probabilities are modeled as a linear function of the Xi.

\operatorname{logit}(p_i)=\ln\left(\frac{p_i}{1-p_i}\right) = \beta_0 %2B \beta_1 x_{1,i} %2B \cdots %2B \beta_k x_{k,i}.

Note that a particular element of Xi can be set to 1 for all i to yield an intercept in the model. The unknown parameters βj are usually estimated by maximum likelihood using a method common to all generalized linear models. The maximum likelihood estimates can be computed numerically by using iteratively reweighted least squares.

The interpretation of the βj parameter estimates is as the additive effect on the log of the odds for a unit change in the jth explanatory variable. In the case of a dichotomous explanatory variable, for instance gender, 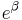e^\beta is the estimate of the odds of having the outcome for, say, males compared with females.

The model has an equivalent formulation

p_i = \frac{1}{1%2Be^{-(\beta_0 %2B \beta_1 x_{1,i} %2B \cdots %2B \beta_k x_{k,i})}}. \,

This functional form is commonly called a single-layer perceptron or single-layer artificial neural network. A single-layer neural network computes a continuous output instead of a step function. The derivative of pi with respect to X = x1...xk is computed from the general form:

y = \frac{1}{1%2Be^{-f(X)}}

where f(X) is an analytic function in X. With this choice, the single-layer neural network is identical to the logistic regression model. This function has a continuous derivative, which allows it to be used in backpropagation. This function is also preferred because its derivative is easily calculated:

\frac{\mathrm{d}y}{\mathrm{d}X} = y(1-y)\frac{\mathrm{d}f}{\mathrm{d}X}. \,

Extensions

Extensions of the model cope with dependent variables with more than two values, also called polytomous regression. Ordered logistic regression handles ordinal dependent variables (ordered values). Multinomial logistic regression handles nominal dependent variables (unordered values, also called "classification"). An extension of the logistic model to sets of interdependent variables is the conditional random field.

Model accuracy

A way to test for errors in models created by step-wise regression is to not rely on the model's F-statistic, significance, or multiple-r, but instead assess the model against a set of data that was not used to create the model.[4] The class of techniques is called cross-validation.

Accuracy is measured as correctly classified records in the holdout sample.[5] There are four possible classifications:

  1. prediction of 0 when the holdout sample has a 0 (True Negative/TN)
  2. prediction of 0 when the holdout sample has a 1 (False Negative/FN)
  3. prediction of 1 when the holdout sample has a 0 (False Positive/FP)
  4. prediction of 1 when the holdout sample has a 1 (True Positive/TP)

These classifications are used to measure Precision and Recall:

\text{Precision}=\frac{tp}{tp%2Bfp} \,
\text{Recall}=\frac{tp}{tp%2Bfn} \,

The percent of correctly classified observations in the holdout sample is referred to the assessed model accuracy. Additional accuracy can be expressed as the model's ability to correctly classify 0, or the ability to correctly classify 1 in the holdout dataset. The holdout model assessment method is particularly valuable when data are collected in different settings (e.g., at different times or places) or when models are assumed to be generalizable.

See also

References

  1. ^ Nemes S, Jonasson JM, Genell A, Steineck G. 2009 Bias in odds ratios by logistic regression modelling and sample size. BMC Medical Research Methodology 9:56 BioMedCentral
  2. ^ Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR (1996). "A simulation study of the number of events per variable in logistic regression analysis". J Clin Epidemiol 49 (12): 1373–9. PMID 8970487. 
  3. ^ Agresti A (2007). "Building and applying logistic regression models". An Introduction to Categorical Data Analysis. Hoboken, New Jersey: Wiley. p. 138. ISBN 978-0-471-22618-5. 
  4. ^ Jonathan Mark and Michael A. Goldberg (2001). Multiple Regression Analysis and Mass Assessment: A Review of the Issues. The Appraisal Journal, Jan. pp. 89–109
  5. ^ Mayers, J.H and Forgy E.W. (1963). The Development of numerical credit evaluation systems. Journal of the American Statistical Association, Vol.58 Issue 303 (Sept) pp 799–806

External links
 
Correlation
Regression analysis
Linear regression
Non-standard predictors
Generalized linear model
Partition of variance